Centro de Estudio Tecnologico del Mar N°26

FISICA

Acuacultura IV

Maestro :Jesus Borrayo


Movimiento Rectelinio Uniforme

• Conceptos de introducción
• Descripción del movimiento rectilíneo uniforme 

  La aceleración es cero (a=0) al no cambiar la velocidad de dirección ni variar su modulo

Por otro lado, la velocidad inicial, media e instantáneadel movimiento tienen el mismo valor en todo momento

Ejemplo
Dos jugadores de canicas se encuentran uno frente a otro con sus canicas en la mano. El juego consiste en lanzarlas al mismo tiempo en línea recta y hacer que ambas se golpeen. Si ambos se encuentran situados a 36 metros uno del otro y el jugador A lanza su canica a 2 m/sg y el jugador B a 4 m/sg en un movimiento rectilíneo uniforme. Calcula a que distancia del jugador B chocarán las canicas.

Datos

Considerando que la canica del jugador A se encuentra en el origen de coordenadas:

Canica A
X0=0 m
VA=2 m/sg

Canica B
X0=36 m
VB=-4 m/sg (se desplaza hacia el origen del sistema de referencia)

n un m.r.u. la posición de un cuerpo en movimiento viene dada por la siguiente ecuación:

x=x0+v⋅t

Canica jugador A.

Sustituyendo los valores de este jugador en la ecuación del m.r.u. obtenemos que:

xA=0+2⋅t m ⇒xA=2⋅t m

Canica jugador B

Sustituyendo nuevamente en la ecuación, pero con los datos del jugador B:

xB=36−4⋅t m

Observa que al desplazarse hacia el origen de nuestro sistema de referencia su velocidad es negativa.

Ambas canicas impactarán cuando sus posiciones sean las mismas, es decir XA=XB, por tanto:

XA=XB⇒2⋅t=36−4⋅t⇒t=366⇒t=6 sg

Es decir, cuando transcurran 6 sg chocarán, pero ¿donde?. Como sabemos cuando se produce el impacto, basta sustituir ese tiempo en la ecuación de la posición de cualquiera de las 2 canicas.

XA=2⋅t⇒XA=2⋅6⇒XA=12 m

Por tanto, el choque se produce a 12 metros del jugador A y a 24 m (36-12) del jugador B.

MOVIMIENTO RECTILÍNEO ACELERADO 

ontrar el movimiento rectilíneo uniformemente acelerado (m.r.u.a.) o movimiento rectilíneo uniformemente variado (m.r.u.v.) en tu día a día es bastante común. Por ejemplo, si dejas caer una moneda al suelo (caida libre), esta realizará un movimiento rectilíneo uniformemente acelerado (m.r.u.a.) omovimiento rectilíneo uniformemente variado (m.r.u.v.). En este apartado vamos a estudiar las ecuaciones y las gráficas que definen a este movimiento.

• Aceleración 

Un motorista que circula a 50 Km/h, sigue una trayectoria rectilínea hasta que acciona los frenos de su vehículo y se detiene completamente. Si desde que frena hasta que se para transcurren 6 segundos, calcula:

 Pregunta:La velocidad con que se movía transcurridos 3 segundos desde que comenzó a frenar.

Datos

Velocidad Inicial. v0 = 50 Km/h = 50 · (1000/3600) = 13.89 m/s
Velocidad Final. vf = 0 Km/h = 0 m/s
Δt = 6 s
a = ?

Resolución

Dado que conocemos la velocidad en dos instantes (v0 y vf)  y el intervalo de tiempo que transcurre entre ellos (6 s), podemos aplicar la definición de aceleración para calcular como varía la velocidad en ese intervalo.

Cuestión 

Datos

v0 = 13.89 m/s
a = 2.31 m/s2
t = 3 s
v = ?

Resolución

Con los datos que tenemos, sustituimos en la ecuación de la velocidad propia de los m.r.u.a. y resolveremos la cuestión: 

v=v0+a⋅t⇒v=13.89 m/s− 2.31m/s2⋅3 s⇒






v=6.96 m/s
  a=Δ           Δ  t=vf−v0Δt⇒a=−13.89 ms/6 s=−2.31 ms2a=ΔvΔt=vf−v0Δt⇒a=−13.89 ms/6 s=−2.31 ms2a=ΔvΔt=vf−v0Δt⇒a=−13.89 ms/6 s=−2.31 ms2a=ΔvΔt=vf−v0Δt⇒a=−13.89 ms/6 s=−2.31 ms2a=ΔvΔt=vf−v0Δt⇒a=−13.89 ms/6 s=−2.31 ms2a=ΔvΔt=vf−v0Δt⇒a=−13.89 ms/6 s=−2.31 ms2a=ΔvΔt=vf−v0Δt⇒a=−13.89 ms/6 s=−2.31 ms2

a=ΔvΔt=vf−v0Δt⇒a=−13.89 ms/6 s=−2.31 ms2

ΔvΔt=vf−v0Δt⇒a=−13.89 ms/6 s=−2.31 ms

ΔvΔt=vf−v0Δt⇒a=−13.89 ms/6 s=−2.31 ms

• Lanzamiento vertical 

De entre todos los movimientos rectilíneos uniformemente acelerados (m.r.u.a.) o movimientos rectilíneos uniformemente variados (m.r.u.v.) que se dan en la naturaleza, existen dos de particular interés: la caída libre y el lanzamiento vertical. En este apartado estudiaremos el lanzamiento vertical. Ambos se rigen por las ecuaciones propias de los movimientos rectilíneos uniformemente acelerados (m.r.u.a.) o movimientos rectilíneos uniformemente variados (m.r.u.v.):

Un equilibrista novato se encuentra sobre una plataforma situada a 12 metros de altura. Practicando juegos malabares con 2 bolas, tiene un traspiés y lanza verticalmente cada una de ellas a 9 m/s, sin embargo una de ellas hacia arriba y que llamaremos A y otra hacia abajo que llamaremos B. Considerando que la gravedad es 10 m/sg2, calcular:

Pregunta: El tiempo que permanecen en el aire..

Datos

H = 12 m
v0 = 9 m/s
g = 10 m/s

Resolución

En ambos casos, para calcular el tiempo que permanecen en el aire deberemos conocer el instante en el que tocan el suelo, es decir cuando su posición y=0 m. Sustituyendo en las ecuaciones de posición del movimiento vertical:

Bola A

yA=H+v0⋅tA−12⋅g⋅tA2⇒0=12+9⋅tA−10⋅tA22⇒0=12+9⋅tA−5⋅tA2⇒tA=2.69 s

Bola B

yB=H+v0⋅tB−12⋅g⋅tB2⇒0=12−9⋅tB−10⋅tB22⇒0=12−9⋅tB−5⋅tB2⇒tB=0.9 s

•  Caída Libre

De entre todos los movimientos rectilíneos uniformemente acelerados (m.r.u.a.) o movimientos rectilíneos uniformemente variados (m.r.u.v.) que se dan en la naturaleza, existen dos de particular interés: la caída libre y el lanzamiento vertical. En este apartado estudiaremos la caída libre. Ambos se rigen por las ecuaciones propias de los movimientos rectilíneos uniformes avanzados  (m.r.u.a.) o movimientos rectilíneos uniformemente variados (m.r.u.v.):

Ejemplo :Un vaso de agua situado al borde de una mesa cae hacia el suelo desde una altura de 1.5 m. Considerando que la gravedad es de 10 m/s2, calcular:

Pregunta:El tiempo que está el vaso en el aire.

Cuestión a)

Datos

H = 1.5 m
Cuando llegue al suelo y = 0 m.
g = 10 m/s2

Resolución

Para resolver esta cuestión basta con aplicar la ecuación de la posición en caída libre y despejar el tiempo cuando el vaso se encuentra en la posición y = 0 m, es decir, cuando ha llegado al suelo:

y=H−g⋅t22⇒t=−2⋅(y−H)g−−−−−−−−−−−√⇒t=−2⋅(0−1.5)10−−−−−−−−−−−−√⇒t=310−−−√⇒t=0.55

•   Movimiento de proyectiles  

es un ejemplo de composición de movimientos en dos dimensiones: un m.r.u. en el eje horizontal y un m.r.u.a. en el vertical. En este apartado veremos:

Ejemplo:Una pelota de tenis situada a 2 metros de altura es golpeada por un jugador con su raqueta. La pelota sale despedida horizontalmente con una velocidad de 30 m/s. Responde a las siguientes preguntas:

Pregunta ¿Cuanto tiempo tarda la pelota en llegar al suelo?

La pelota llegará al suelo cuando su posición Y sea 0 (y=0). Según las ecuaciones del lanzamiento horizontal:

y=H−12⋅g⋅t2⇒0=2 m−0.5⋅9.8 ms2/⋅t2⇒t=0.63 s

Movimiento Circular 

• Movimiento circular uniforme 

Un cuerpo realiza un movimiento circular uniforme (m.c.u.) cuando su trayectoria es una circunferencia y su velocidad angular es constante.

Un cuerpo describe un movimiento circular uniforme de 3 metros de radio. ¿Cuál es su vector de posición cuando su posición angular es de 30º?

Datos

R = 3 m
φ = 30º = 1/6 π rad

Resolución

Sabiendo que el vector de posición de un cuerpo en un movimiento circular uniforme (m.c.u.) se obtiene por medio de la siguiente expresión:

r→=x⋅i→+y⋅j→=R⋅cos(φ)⋅i→+R⋅sin(φ)⋅j→

Basta con sustituir en esta ecuación los datos que conocemos:

r→=3⋅cos (16/⋅π)⋅i→+3⋅sin (16/⋅π)⋅j→ ⇒r→=2.6 ⋅ i→ + 1.5 ⋅ j →

• Movimiento circular acelerado 

Un cuerpo realiza un movimiento circular uniformemente acelerado (m.c.u.a.) cuando su trayectoria es una circunferencia y su aceleración angular es constante

Masa y peso 

• Masa 

Encuentra el centro de masas de las partículas que aparecen en la figura. Se supone que el sistema es rígido y el sistema de referencia se encuentra expresado en metros.

---

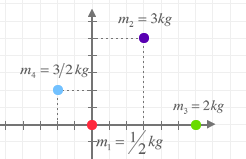
Datos

• m1 = 1/2 kg
• m2 = 3 kg
• m3 = 2 kg
• m4 = 3/2 kg
• r→1=0 m
• r→2=3⋅i→+5⋅j→ m
• r→3=6⋅i→ 
• r→4=−2⋅i→+2⋅j→ m

Consideraciones previas

• Se nos indica que las distancias entre las partículas son rígidas. Es por tanto un sólido rígido y tiene sentido que nos preguntemos por el centro de masas.
• Todas las partículas se encuentran en un plano, por lo que podemos despreciar la coordenada z (z = 0 en todas)

Resolución

La posición del centro de masas viene dada por:

r→CM=∑i=1nmi⋅r→imtotal=m1⋅r→1+m2⋅r→2+…+mn⋅r→nm1+m2+…+mn

Por tanto, aplicando a nuestras 4 partículas, separando las coordenadas x e y nos queda:

xCM=m1⋅x1+m2⋅x2+m3⋅x3+m4⋅x4m1+m2+m3+m4=12⋅0+3⋅3+2⋅6+32⋅(−2)12+3+2+32=187 myCM=m1⋅y1+m2⋅y2+m3⋅y3+m4⋅y4m1+m2+m3+m4=12⋅0+3⋅5+2⋅0+32⋅(2)12+3+2+32=187 m

Es decir, el vector de poción del centro de masas es:

r→CM=187⋅i→+187⋅j→m=(187,187) m

---

• Peso

El peso (P) de un cuerpo en un punto es la fuerza gravitatoria  que actúa sobre él. Su unidad en el S.I. es el Newton (N) y matemáticamente se expresa como:

P→=−G⋅M⋅mr2⋅u→r

¿Cuál será el peso de una persona de 70 kg en la superficie de la Tierra y a 500 km de altura?. Masa de la Tierra: 6·1024 kg. Radio de la Tierra: 6370 Km.

---

Datos

h = 500 km = 500 · 103 m
m = 70 kg
MT= 6·1024 kg
RT=6370 Km = 6.37 · 106 m

Resolución

En la Supercie de la Tierra

Aplicando la definición de peso en el superficie de la Tierra, obtenemos que:

P=m⋅g ⇒P=70⋅9.8 ⇒P=686 N

A 500 Km sobre la Superficie de la Tierra

Para calcular el peso a la altura que se nos solicita, debemos utilizar la definición genérica del peso, sabiendo que la distancia que separa a la persona y el centro de la tierra es (RT+h):

P=G⋅MT⋅m(RT+h)2 ⇒P=6.67⋅10−11⋅6⋅1024⋅70(6.37⋅106+500⋅103)2 ⇒P=6.67⋅10−11⋅6⋅1024⋅704.72⋅1013⇒P=6.67⋅10−11⋅8.9⋅1012 ⇒P=593 N

Como puedes observar, cuanto mayor es la altura menor es el peso de la persona. Esto explica que los astronautas en el espacio floten dentro de la nave.

Leyes de newton 

• Primera ley de newton

• segunda ley de newton
• tercera ley de newton 

y=H−12⋅g⋅t2⇒0=2 m−0.5⋅9.8 ms2/⋅t2⇒t=0.63 sUn cuerpo realiza un movimiento circular uniformemente acelerado (m.c.u.a.) cuando su trayectoria es una circunferencia y su aceleración angular es constante