Fisica Acuacultura IV: junio 2019

miércoles, 5 de junio de 2019

Fuerza

Fuerza e interaccion

Se empuja un cajon aplicando cada un una fuerza de paralela al suelo.el primero hace una fuerzza de 50 N y el segundo de 40N formando entre ellos un angulo de 37 grados
cual es la fuerza neta sobre el cajon?
primero debes de elegir los ejes cartesianos descompones las fuerzas segun los ejes y calcula sus componentes
F1x=50N F1Y=0 N
F2x=40 cos 37=32 N
F2y=40 sen 37=24 N
Obtienes las fuerzas resultantes
F=(50+32)(0+24)= 82+24

a=16,3 grados

Fuerza gravitatoria

Calcular la fuerza con que se atraen dos masas de 10 y 300 kg. situadas a una distancia de 50m.

Un ejercicio simple de aplicación de la ley de la fuerza de la gravedad. Lo único que hay que

recordar es la fórmula:

F=G (M ·m./d2

El valor de G es 6,67·10-11 N·m2

/Kg2 (este valor, en principio, te lo darían siempre).

F = 6,67·10-11·(10·300)/502

F = 8·10-11 N

Equilibrio rotacional

Segunda condición de equilibrio

Caso 1:

, basta con observar el brazo de palanca que existe desde donde está la fuerza hasta el punto de apoyo T , hay 15 metros y además una fuerza de 10N, considerando que un momento es positivo si la fuerza apunta en dirección contraria a las manecillas del reloj, y negativo si gira en dirección horaria, entonces sabremos que es un momento negativo.

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( -10N \right)\left( 15m \right)=-150Nm$

Caso 2:

La única diferencia del caso 1, es que la fuerza está en dirección contraria a las manecillas del reloj, por lo que tendremos un momento positivo. Esto es matemáticamente:

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( 10N \right)\left( 15m \right)=150Nm$

Caso 3:

En el caso 3, vemos claramente que la fuerza está en dirección de las manecillas del reloj, por lo cual es negativa, y la distancia donde se aplica la fuerza es a mitad del punto de apoyo T, entonces decimos que:

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( -10N \right)\left( 7.5m \right)=75Nm$

Caso 4:

Este caso es importante, al no haber ningún brazo de palanca “distancia” es lógico que la viga no tendrá ninguna reacción de fuerza, ya que está justamente en el punto de apoyo, ahora matemáticamente podríamos explicarlo así:

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( 10N \right)\left( 0m \right)=0$

Equilibrio tranlacional

Primera condición de equilibrio

Dos cables sostienen un semáforo cuyo peso tiene una magnitud de 240 N, formando un ángulo de 150° con ambas cuerdas, tal como se muestra en la figura. Calcule la magnitud de la fuerza aplicada por cada cable.

Solución:

Elaboramos el diagrama de cuerpo libre de nuestro problema, extrayendo primero las fuerzas que están activas en dicho cuerpo, incluyendo los ángulos.

Como los cables están generando una tensión con los postes que soportan al semáforo, van en dirección a los postes, no al semáforo. El peso del semáforo hace que la fuerza jale hacía abajo. Una vez teniendo en cuenta dicho punto, es momento de realizar un diagrama de cuerpo libre más completo, colocando las fuerzas en el plano cartesiano.

Hemos colocado 15° en los ángulos de las tensiones con la horizontal, ya que el ángulo que había entre cable y cable eran de 150°. Es lógico que los ángulos restantes fueran 30°, ahora vamos a colocar la sumatoria de fuerzas en el eje “x”

$\displaystyle \sum{{{{\vec{F}}}_{x}}}=0$

Observamos por nuestro plano cartesiano, que solamente lo que está de lado derecho es positivo, y de lado izquierdo negativo.

Para el eje “x”

$\displaystyle \sum{{{\overrightarrow{F}}_{x}}}={{\overrightarrow{T}}_{1}}_{x}-{{\overrightarrow{T}}_{2}}_{x}=0$

Para el eje “y”

$\displaystyle \sum{{{\overrightarrow{F}}_{y}}}={{\overrightarrow{T}}_{1}}_{y}+{{\overrightarrow{T}}_{2}}_{y}-P=0$

Resolviendo para el eje “x”

Como bien sabemos, tenemos que descomponer nuestros vectores en su forma rectangular de tal forma que:

$\displaystyle \sum{{{\overrightarrow{F}}_{x}}}={{T}_{1}}\cos 15{}^\circ -{{T}_{2}}\cos 15{}^\circ =0$

Al tratarse de una igualdad, vamos a despejar de tal forma que nos quede así

$\displaystyle {{T}_{1}}\cos 15{}^\circ ={{T}_{2}}\cos 15{}^\circ$

$\displaystyle {{T}_{1}}={{T}_{2}}$

Esto nos da entender, que tanto la tensión 1 como la tensión 2, son iguales. Ahora lo que necesitamos saber es cuanto vale la tensión, y ese dato nos arrojará cuando resolvamos para el eje “y”.

Resolviendo para el eje “y”

$\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{2}}sen15{}^\circ -250N=0$

$\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{2}}sen15{}^\circ =250N$

Pero como sabemos que:

$\displaystyle {{T}_{1}}={{T}_{2}}$

$\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{1}}sen15{}^\circ =250N$

Es decir:

$\displaystyle 2{{T}_{1}}sen15{}^\circ =250N$

Despejando a T1

$\displaystyle {{T}_{1}}=\frac{250N}{2sen15{}^\circ }=482.96N$

Esto quiere decir que tanto T1 como T2 tienen una fuerza de tensión de 482.96 Newtons cada una.

Resultado:

$\displaystyle {{T}_{1}}={{T}_{2}}=482.96N$

Equilibrio rotacional

Segunda condición de equilibro
El momento de una fuerza es positiva si su tendencia de giro respecto a un cuerpo es en sentido contrario al giro de las manecillas del reloj.

Si deseamos encontrar el Momento de cada fuerza lo haríamos de la siguiente forma:

Caso 1:

Para este caso, basta con observar el brazo de palanca que existe desde donde está la fuerza hasta el punto de apoyo T , hay 15 metros y además una fuerza de 10N, considerando que un momento es positivo si la fuerza apunta en dirección contraria a las manecillas del reloj, y negativo si gira en dirección horaria, entonces sabremos que es un momento negativo.

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( -10N \right)\left( 15m \right)=-150Nm$

Caso 2:

La única diferencia del caso 1, es que la fuerza está en dirección contraria a las manecillas del reloj, por lo que tendremos un momento positivo. Esto es matemáticamente:

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( 10N \right)\left( 15m \right)=150Nm$

Caso 3:

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( -10N \right)\left( 7.5m \right)=75Nm$

Caso 4:

$\displaystyle \sum{\overrightarrow{M}}=Fd=\left( 10N \right)\left( 0m \right)=0$

Equilibrio Translacional

Primera condición de equilibrio

Dos cables sostienen un semáforo cuyo peso tiene una magnitud de 240 N, formando un ángulo de 150° con ambas cuerdas, tal como se muestra en la figura. Calcule la magnitud de la fuerza aplicada por cada cable.

Solución:

Elaboramos el diagrama de cuerpo libre de nuestro problema, extrayendo primero las fuerzas que están activas en dicho cuerpo, incluyendo los ángulos.

$\displaystyle \sum{{{{\vec{F}}}_{x}}}=0$

Observamos por nuestro plano cartesiano, que solamente lo que está de lado derecho es positivo, y de lado izquierdo negativo.

Para el eje “x”

$\displaystyle \sum{{{\overrightarrow{F}}_{x}}}={{\overrightarrow{T}}_{1}}_{x}-{{\overrightarrow{T}}_{2}}_{x}=0$

Para el eje “y”

$\displaystyle \sum{{{\overrightarrow{F}}_{y}}}={{\overrightarrow{T}}_{1}}_{y}+{{\overrightarrow{T}}_{2}}_{y}-P=0$

Resolviendo para el eje “x”

Como bien sabemos, tenemos que descomponer nuestros vectores en su forma rectangular de tal forma que:

$\displaystyle \sum{{{\overrightarrow{F}}_{x}}}={{T}_{1}}\cos 15{}^\circ -{{T}_{2}}\cos 15{}^\circ =0$

Al tratarse de una igualdad, vamos a despejar de tal forma que nos quede así:

$\displaystyle {{T}_{1}}\cos 15{}^\circ ={{T}_{2}}\cos 15{}^\circ$

$\displaystyle {{T}_{1}}={{T}_{2}}$

Resolviendo para el eje “y”

$\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{2}}sen15{}^\circ -250N=0$

$\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{2}}sen15{}^\circ =250N$

Pero como sabemos que:

$\displaystyle {{T}_{1}}={{T}_{2}}$

$\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{1}}sen15{}^\circ =250N$

Es decir:

$\displaystyle 2{{T}_{1}}sen15{}^\circ =250N$

Despejando a T1

$\displaystyle {{T}_{1}}=\frac{250N}{2sen15{}^\circ }=482.96N$

Esto quiere decir que tanto T1 como T2 tienen una fuerza de tensión de 482.96 Newtons cada una.

Resultado:

$\displaystyle {{T}_{1}}={{T}_{2}}=482.96N$

Fricción

Fricción estatestática
Fricción Dinámica

Un bloque de acero tiene un peso de 30 N, y éste comienza a deslizarse sobre una superficie totalmente horizontal de madera, con ello se produce una fuerza máxima de fricción estática cuya magnitud es de 15 N, como se observa en la imagen. Calcule el coeficiente de fricción estático entre el acero y la madera

Solución:
Como lo que nos piden es prácticamente el coeficiente de rozamiento de fricción estática, solamente debemos recordar que en nuestra fórmula es la razón entre la fuerza estática máxima y la normal, dichos datos los tenemos:
Ue=Fe(max)/N=15N/30N=0.5

Lo que vendría a ser nuestro coeficiente de fricción estático entre la madera y el acero.

Dinámica

Calcular la fuerza necesaria que se necesita aplicar a un mueble cuyo peso es de 450 N para poder deslizarlo a una velocidad constante horizontalmente, donde el coeficiente de fricción dinámico es de 0.43 .

Solución:

En este caso nos proporcionan el coeficiente de fricción dinámico, además del peso del mueble, es lógico que tendremos que utilizar la fórmula de la fuerza de fricción dinámica (ya que es opuesta a la fuerza que jala el objeto).

Nota: El valor de la fuerza normal (N) actúa en dirección al peso, es por eso que la fuerza normal tendrá el mismo valor que el peso. Si el mueble estuviera en un plano inclinado, entonces el problema tendría más procedimientos, ya que tendríamos que descomponer en forma rectangular a los vectores del peso, para poder encontrar la normal.

Bueno asumiendo lo dicho anteriormente, tendríamos que aplicar nuestra fórmula:

Fd=UdN

Sustituyendo datos:
Fd(0.3)(450N)=193.5N

Por lo que la fuerza de fricción dinámica será de 193.5 N, con esto solucionamos el problema.

Primera ley de newton

Uno de los más comunes es cuando vamos en un transporte (automóvil o camión), y de pronto frena: el vehículo se detiene, pero nosotros, aunque vayamos sentados, seguimos moviéndonos hacia adelante, porque, aunque no lo sintamos, estamos siguiendo el mismo movimiento del vehículo, y al detenerse de pronto, nuestro cuerpo sigue la misma trayectoria que estaba recorriendo.

Otro ejemplo es cuando nos tropezamos. En lugar de detenerse todo nuestro cuerpo, nuestra parte superior sigue la inercia del movimiento que llevábamos, mientras que nuestros pies se detienen súbitamente, es por ello que nuestro cuerpo sigue el sentido del movimiento.

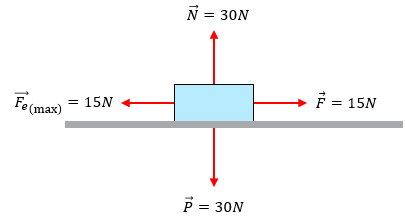
Un ejemplo de lo contrario, es cuando estamos parados y alguien nos empuja. Estando de pie, sin movernos, nuestro equilibrio es la posición estática, y el empujón es la fuerza que cambia nuestro estado de reposo por el de movimiento, haciéndonos correr o que nos caigamos.

segunda ley de newton

1. Una fuerza le proporciona a la masa de 2,5 Kg. una aceleración de 1,2 m/s2. Calcular la magnitud de dicha fuerza en Newton y dinas.

Datos

m = 2,5 Kg.

a =1,2 m/s2.

F =? (N y dyn)

Solución

Nótese que los datos aparecen en un mismo sistema de unidades (M.K.S.)

Para calcular la fuerza usamos la ecuación de la segunda ley de Newton:

F=M.A

Sustituyendo valores tenemos:

F=2.5K 1,2m/s2=3K.m/s2

F=3n

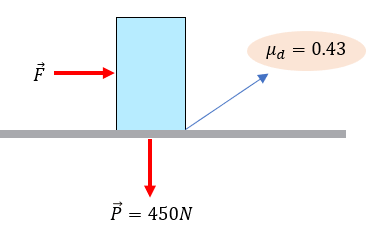
Resultado de imagen para Una fuerza le proporciona a la masa de 2,5 Kg. una aceleraciÃ³n de 1,2 m/s2

tercera ley de newton

La ley de la acción y la reacción es bastante sencilla, cuando hablamos de un objeto que choca contra un muro, o dos objetos que tienen la misma masa. Sin embargo, si combinamos la fórmula de la tercera ley de Newton: F1 = –F2, con la fórmula de la segunda ley: F = ma, entonces podemos calcular qué pasará con objetos de diferentes masas.

Así lo podemos calcular si tenemos en cuenta que (F = ma)1 = –(F = ma)2. Esto nos permite hacer cálculo como los siguientes:

Calcular la masa del objeto 1, si con una aceleración de 2 m/s, produce una fuerza de 0.25 N, y calcular la aceleración del objeto 2, si su masa es de 250 gramos.

Calculando con la segunda ley de Newton el objeto 1:

F= 0.25 N
a= 2m/s2m = F/a = 0.25/2 = 0.125kg = 125 gramos

Ley de gravitación universal.

1. Hallar la fuerza con que se atraen dos masas de 5,5 ( 1024 Kg. y 7,3 ( 1022 Kg. separados por una distancia de 3,8 ( 108 m.

Solución

F = ?

M1 = 5,5 . 1024 Kg.

M2 = 7,3 . 1022 Kg.

d = 3,8 . 108 m

G=6.67(-11) N.n2/Kg2

Para calcular la fuerza de atracción entre las masas M1 y M2, sustituimos en la fórmula de la cuarta ley de Newton el valor de cada una de ellas, así como los valores de G, y de la distancia d:

Fg=G M1.M2/d2

Q0uedando la fórmula como sigue:

F=6,67x10(-11)N./Kg2 2,78x10(50)Kg/M2

F=18,55X(19)N

Masa y peso

• Masa

Encuentra el centro de masas de las partículas que aparecen en la figura. Se supone que el sistema es rígido y el sistema de referencia se encuentra expresado en metros.o

Datos

m1 = 1/2 kg

m2 = 3 kg

m3 = 2 kg

m4 = 3/2 kg

r→1=0 m

r→2=3⋅i→+5⋅j→ m

r→3=6⋅i→

r→4=−2⋅i→+2⋅j→ m

Consideraciones previas

· Se nos indica que las distancias entre las partículas son rígidas. Es por tanto un sólido rígido y tiene sentido que nos preguntemos por el centro de masas

· Todas las partículas se encuentran en un plano, por lo que podemos despreciar la coordenada z (z = 0 en todas)

Resolución

La posición del centro de masas viene dada por:

r→CM=∑i=1nmi⋅r→imtotal=m1⋅r→1+m2⋅r→2+…+mn⋅r→nm1+m2+…+mn

Por tanto, aplicando a nuestras 4 partículas, separando las coordenadas x e y nos queda:

xCM=m1⋅x1+m2⋅x2+m3⋅x3+m4⋅x4m1+m2+m3+m4=12⋅0+3⋅3+2⋅6+32⋅(−2)12+3+2+32=187 myCM=m1⋅y1+m2⋅y2+m3⋅y3+m4⋅y4m1+m2+m3+m4=12⋅0+3⋅5+2⋅0+32⋅(2)12+3+2+32=187 m

Es decir, el vector de poción del centro de masas es:

r→CM=187⋅i→+187⋅j→m=(187,187) m

· Peso

El peso (P) de un cuerpo en un punto es la fuerza gravitatoria que actúa sobre él. Su unidad en el S.I. es el Newton (N) y matemáticamente se expresa como:

P→=−G⋅M⋅mr2⋅u→r

¿Cuál será el peso de una persona de 70 kg en la superficie de la Tierra y a 500 km de altura?. Masa de la Tierra: 6·1024 kg. Radio de la Tierra: 6370 Km.

Datos

h = 500 km = 500 · 103 m

m = 70 kg

MT= 6·1024 kg

RT=6370 Km = 6.37 · 106 m

Resolución

En la Supercie de la Tierra

Aplicando la definición de peso en el superficie de la Tierra, obtenemos que:

P=m⋅g ⇒P=70⋅9.8 ⇒P=686 N

A 500 Km sobre la Superficie de la Tierra

Para calcular el peso a la altura que se nos solicita, debemos utilizar la definición genérica del peso, sabiendo que la distancia que separa a la persona y el centro de la tierra es (RT+h):

P=G⋅MT⋅m(RT+h)2 ⇒P=6.67⋅10−11⋅6⋅1024⋅70(6.37⋅106+500⋅103)2 ⇒P=6.67⋅10−11⋅6⋅1024⋅704.72⋅1013⇒P=6.67⋅10−11⋅8.9⋅1012 ⇒P=593 N