Masa y peso
• Masa
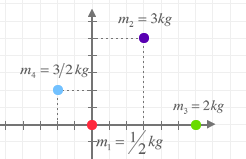
Encuentra el centro de masas de las partículas que aparecen en la figura. Se supone que el sistema es rígido y el sistema de referencia se encuentra expresado en metros.o
Datos
m1 = 1/2 kg
m2 = 3 kg
m3 = 2 kg
m4 = 3/2 kg
r→1=0 m
r→2=3⋅i→+5⋅j→ m
r→3=6⋅i→
r→4=−2⋅i→+2⋅j→ m
Consideraciones previas
·
Se nos indica que las distancias entre las partículas son rígidas. Es por
tanto un sólido rígido y tiene sentido que nos preguntemos por el centro de masas
·
Todas las partículas se encuentran en un plano, por lo que podemos
despreciar la coordenada z (z = 0 en todas)
Resolución
La posición del centro
de masas viene dada por:
r→CM=∑i=1nmi⋅r→imtotal=m1⋅r→1+m2⋅r→2+…+mn⋅r→nm1+m2+…+mn
Por tanto, aplicando a
nuestras 4 partículas, separando las coordenadas x e y nos
queda:
xCM=m1⋅x1+m2⋅x2+m3⋅x3+m4⋅x4m1+m2+m3+m4=12⋅0+3⋅3+2⋅6+32⋅(−2)12+3+2+32=187 myCM=m1⋅y1+m2⋅y2+m3⋅y3+m4⋅y4m1+m2+m3+m4=12⋅0+3⋅5+2⋅0+32⋅(2)12+3+2+32=187 m
Es decir, el vector de
poción del centro de masas es:
r→CM=187⋅i→+187⋅j→m=(187,187) m
·
Peso
El peso (P) de un cuerpo en un punto es la fuerza gravitatoria que
actúa sobre él. Su unidad en el S.I. es el Newton (N) y
matemáticamente se expresa como:
P→=−G⋅M⋅mr2⋅u→r
¿Cuál será el peso de una persona de 70 kg en la superficie de la Tierra y
a 500 km de altura?. Masa de la Tierra: 6·1024 kg. Radio de la Tierra: 6370 Km.
Datos
h = 500 km = 500 · 103 m
m = 70 kg
MT= 6·1024 kg
RT=6370 Km = 6.37 · 106 m
Resolución
En la Supercie de la
Tierra
Aplicando la definición
de peso en el superficie de la Tierra,
obtenemos que:
P=m⋅g ⇒P=70⋅9.8 ⇒P=686 N
A 500 Km sobre la
Superficie de la Tierra
Para calcular el peso a
la altura que se nos solicita, debemos utilizar la definición genérica del
peso, sabiendo que la distancia que separa a la persona y el centro de la
tierra es (RT+h):
P=G⋅MT⋅m(RT+h)2 ⇒P=6.67⋅10−11⋅6⋅1024⋅70(6.37⋅106+500⋅103)2 ⇒P=6.67⋅10−11⋅6⋅1024⋅704.72⋅1013⇒P=6.67⋅10−11⋅8.9⋅1012 ⇒P=593 N

No hay comentarios:
Publicar un comentario