Fisica Acuacultura IV

Equilibrio Translacional

Primera condición de equilibrio

Dos cables sostienen un semáforo cuyo peso tiene una magnitud de 240 N, formando un ángulo de 150° con ambas cuerdas, tal como se muestra en la figura. Calcule la magnitud de la fuerza aplicada por cada cable.

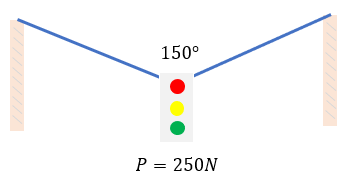
Solución:

Elaboramos el diagrama de cuerpo libre de nuestro problema, extrayendo primero las fuerzas que están activas en dicho cuerpo, incluyendo los ángulos.

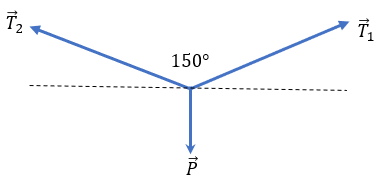
Como los cables están generando una tensión con los postes que soportan al semáforo, van en dirección a los postes, no al semáforo. El peso del semáforo hace que la fuerza jale hacía abajo. Una vez teniendo en cuenta dicho punto, es momento de realizar un diagrama de cuerpo libre más completo, colocando las fuerzas en el plano cartesiano.

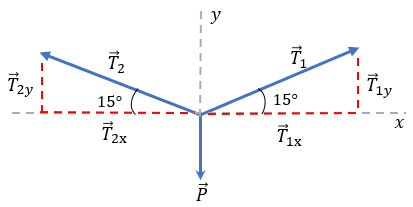
Hemos colocado 15° en los ángulos de las tensiones con la horizontal, ya que el ángulo que había entre cable y cable eran de 150°. Es lógico que los ángulos restantes fueran 30°, ahora vamos a colocar la sumatoria de fuerzas en el eje “x”

$\displaystyle \sum{{{{\vec{F}}}_{x}}}=0$

Observamos por nuestro plano cartesiano, que solamente lo que está de lado derecho es positivo, y de lado izquierdo negativo.

Para el eje “x”

$\displaystyle \sum{{{\overrightarrow{F}}_{x}}}={{\overrightarrow{T}}_{1}}_{x}-{{\overrightarrow{T}}_{2}}_{x}=0$

Para el eje “y”

$\displaystyle \sum{{{\overrightarrow{F}}_{y}}}={{\overrightarrow{T}}_{1}}_{y}+{{\overrightarrow{T}}_{2}}_{y}-P=0$

Resolviendo para el eje “x”

Como bien sabemos, tenemos que descomponer nuestros vectores en su forma rectangular de tal forma que:

$\displaystyle \sum{{{\overrightarrow{F}}_{x}}}={{T}_{1}}\cos 15{}^\circ -{{T}_{2}}\cos 15{}^\circ =0$

Al tratarse de una igualdad, vamos a despejar de tal forma que nos quede así:

$\displaystyle {{T}_{1}}\cos 15{}^\circ ={{T}_{2}}\cos 15{}^\circ$

$\displaystyle {{T}_{1}}={{T}_{2}}$

Esto nos da entender, que tanto la tensión 1 como la tensión 2, son iguales. Ahora lo que necesitamos saber es cuanto vale la tensión, y ese dato nos arrojará cuando resolvamos para el eje “y”.

Resolviendo para el eje “y”

$\displaystyle {{T}_{1}}sen15{}^\circ +{{T}_{2}}sen15{}^\circ -250N=0$